Overview
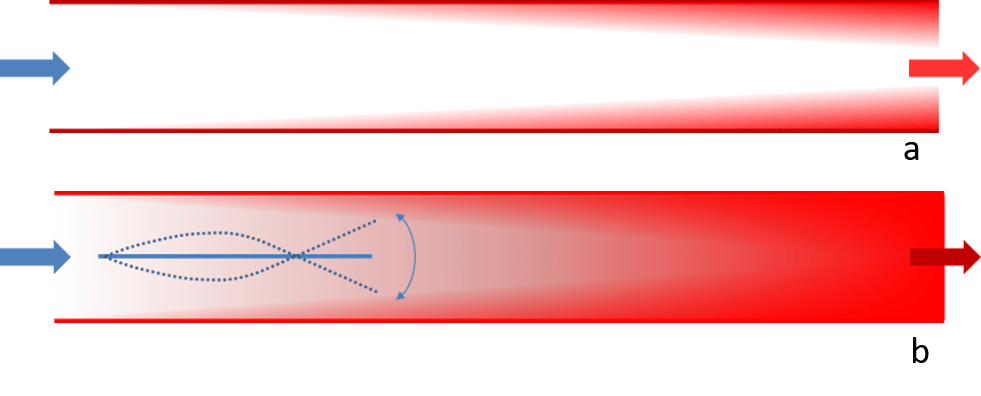
Forced convection heat transfer in compact, high-power, air-cooled heat sinks with high density, high aspect ratio fin channels is typically limited by low channel Reynolds number (Re) laminar flow that is associated with the available volume flow rate. As a result of the low Re, heat transfer is restricted by the coupled local heat transfer from the fin surfaces within thin thermal boundary layers and by insufficient mixing of the wall-bound heated air with the core flow as shown schematically in Figure 1a. These limitations are commonly overcome by increasing the air volume flow rate, the fin planform dimensions and density, or by passive channel obstructions such as vortex generators and dimples but are accompanied by significant penalties in the form of increased flow losses. The current work focuses on overcoming these limitations by inducing small-scale motions and increasing the mixing throughout the channel using self-oscillating reeds.
Small-Scale Generation Mechanisms
Figure 2. Color raster plots of the spanwise vorticity phase-locked to reed motion at the reed’s spanwise center plane along the reed surface and downstream of the reed ( Length = 50 mm, thickness = 38 μm and span =23 mm) placed in a channel with 25×25 mm cross-section and 250 mm length.
The interactions between the reed and the channel flow lead to the formation, evolution, and dissipation of a hierarchy of small-scale motions which can be measured using point and field measurement techniques such as hot-wire anemometry and particle image velocimetry (PIV). Figure 2 shows the color raster plots of the spanwise vorticity along with velocity field on the reed and downstream of the reed, phase locked to the motion of the reed at it spanwise centerline (as indicated in red) obtained using 2-D low-speed PIV. The concave and convex shapes of the reed at its root drive the formation of reed bound spanwise vorticity filaments of clockwise and counterclockwise sign. These vorticity filaments are then advected by the reed undulations and finally shed at its tip. The reed brings vorticity of opposite sign to that of the wall which leads to modulation of the wall boundary layer and as the reed moves away from the wall, it mixes the wall bound flow with the core flow. Both these processes enhance the mixing within the channel. The interactions between the shed vorticity, the wall, and flow downstream of the reed lead to the formation of small-scale motions which enhance the heat transfer within the channel.
Thermal Performance Enhancement Using Reeds
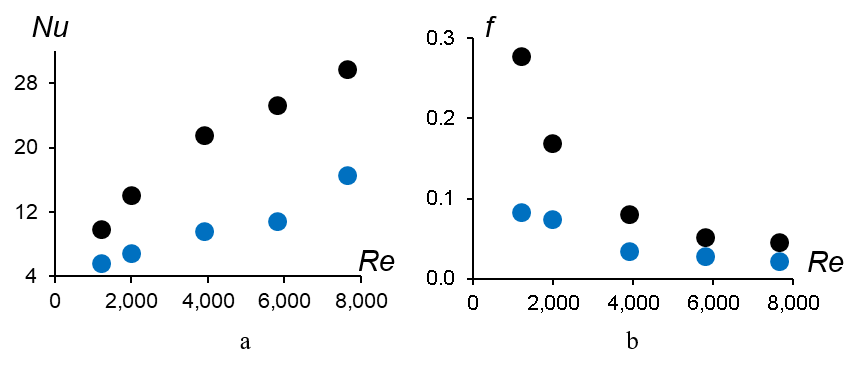
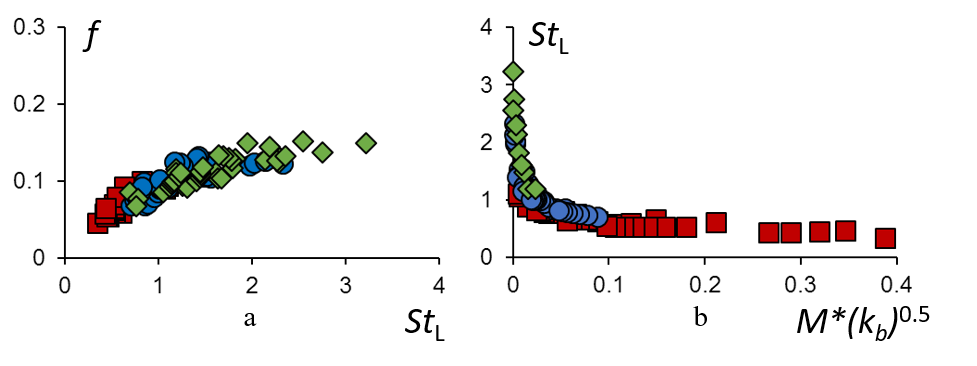
The channel heat transfer as measured through the normalized heat transfer coefficient, Nu, and its variation with the normalized channel flow speed, Re, in the absence (baseline) and presence of the reed (fixed length) is shown in Figure 3a. The reed enhances heat transfer as compared to the baseline for 1,000 < Re < 10,000 with the maximum Nu enhancement of up to 130%. The reed driven heat transfer enhancement is accompanied by a marginal increment in channel flow losses (as measured by the friction factor, f, shown in Figure 3b) due to the flow power required to drive the reed and associated small-scale motions. The channel flow losses are strongly dependent on oscillating frequency of the reed as measured by its Strouhal number, StL (Figure 4a) and therefore can be controlled by reducing the operating Strouhal number. It has been shown in the current study that such reduction in StL has a negligible effect on the reed’s heat transfer enhancement. The reed StL can be reduced by careful selection of its mass ratio (M*=ρsL/(ρat), ρs and ρa being the density of the reed and airflow and L and t being the length and thickness of the reed) and normalized bending rigidity (kb* = kb/(0.5ρaU2L3), kb being the bending rigidity of the reed) as shown in Figure 4b.
The reed technology therefore offers a unique flow control platform to obtain an optimal thermal performance enhancement (i.e. high heat transfer enhancement at low channel loss increment). This makes the reeds suitable for implementation in low Re air-cooling systems where both high heat transfer and low cooling power are critical such as air-cooled condensers of thermo-electric power plants and heat exchangers used in chemical processing industries as well as high-performance heat sinks used in data centers. A Georgia Tech study has shown that the implementation of reeds can improve the overall system level performance of air-cooled condensers and thermo-electric power plants with up to 17% reduction in air blower power and 0.32% increment in efficiency of a thermal power plant.
Supported by AFOSR, NSF-EPRI and RAPID
